![[Previous]](zleft.gif){kind=small}
![[Contents]](zup.gif){kind=small}
![[Next]](zright.gif){kind=small}
|
|
|
|
|
Each race has a "peak arrival rate" which may also be expressed in runners per minute. If runners arrive at the finish line at a rate significantly greater than the processing rate, they will "build-up" in the processing chutes (if they don't back up across the finish line). We will show that allowing runners to build-up in the chutes is NOT the best way to go and, in fact, is the way to disaster.
Ideally, your processing system should be capable of handling the peak arrival rate without allowing runners to stand in the chutes awaiting processing. In fact, the BEST systems are designed to KEEP RUNNERS MOVING.
The remainder of this chapter will deal with the problems of estimating peak finishing rates, chute build-up, finish line back-up, ideal chute length, and the theory of the "wave" start for handling "mega-races."
Although the actual peak arrival rate varies from race to race, a good (conservative) estimate of the peak arrival rate is:
EQUATION (1)
P = 0.6 N/D
where N is the total number of finishers in the race and D is the race distance in kilometers. The peak arrival rate is then the number of finishers to be expected in the peak minute. This formula usually OVERESTIMATES the actual peak minute, especially for very large races where road-way width also limits the rate at which runners can pass by any given point. Equation (1) may UNDERESTIMATE the actual peak minute for elite or restricted entry fields and/or exceptionally "fast" courses such as down-hill courses.
For example, in the 1985 Perrier race, there were 3080 men finishers. Equation (1) predicts a peak arrival rate of 0.6 x 3080 / 10 or 184.8 runners per minute. The observed peak arrival rate (from the diagram) is 175 rpm. For the Elizabeth River Run, there were 3061 finishers for a calculated peak arrival rate of 183.7 rpm. The observed peak arrival rate was 165 rpm.
Obviously, in planning a race, you do not know the exact number of finishers. In such cases, you should use the number of entrants since this will be larger than the actual number of finishers unless you have a very high percentage of "interlopers" or unregistered runners. Note that it is recommended to PROCESS interlopers which means they "count" toward your peak arrival rate.
Table I is derived from equation (1) forvarious race distances and sizes. The peak arrival rates are given in "runners per minute" which is abbreviated "rpm." Peak arrival rates for 20 km may be used for a half-marathon and those for 15 km may be used for a 10 mile race.
5km 8km 10km 12km 15km 20km 25km 30km Mara
(size)
500 60 38 30 25 20 15 12 10 7
1000 120 75 60 50 40 30 24 20 14
1500 180 113 90 75 60 45 36 30 21
2000 240 150 120 100 80 60 48 40 28
2500 300 188 150 125 100 75 60 50 36
3000 360 225 180 150 120 90 72 60 43
4000 480 300 240 200 160 120 96 80 57
5000 600 375 300 250 200 150 120 100 71
6000 720 450 360 300 240 180 144 120 85
8000 960 600 480 400 320 240 192 160 114
10000 1200 750 600 500 400 300 240 200 142
15000 1800 1125 900 750 600 450 360 300 213
20000 2400 1500 1200 1000 800 600 480 400 284
25000 3000 1875 1500 1250 1000 750 600 500 355
30000 3600 2250 1800 1500 1200 900 720 600 427
40000 4800 3000 2400 2000 1600 1200 960 800 569
Single Finish Line Multi Finish Line
If the processing rate or the rate at which runners are removed from the chutes (R) is less than the peak arrival rate (P), you can expect a build-up of runners awaiting processing. This usually occurs when runners are waiting (in the chutes) to be recorded rather than waiting to be timed since recording or collecting bib- number information is usually slower than timing. The greater the discrepancy between the peak arrival rate and the processing (removal) rate, the greater the build-up.
Given a set of race finish results, determining the build-up of runners awaiting processing can be determined for a variety of assumed processing rates. Consider the 1985 Elizabeth River Run, a mixed race with 3061 finishers. In the following table, the number of finishers arriving in the preceding minute is given for each minute from 38 to 64 minutes. Chute build-up for processing rates of 160, 140, 120, 100, and 80 rpm is given.
Time # arriving R = 160 R = 140 R = 120 R = 100 R = 80 (min) in past min 38 64 0 0 0 0 0 39 77 0 0 0 0 0 40 93 0 0 0 0 13 41 96 0 0 0 0 29 42 88 0 0 0 0 37 43 110 0 0 0 10 67 44 133 0 0 13 43 120 45 145 0 5 38 88 185 46 148 0 13 66 136 253 47 165 5 38 111 201 338 48 158 3 56 149 259 416 49 153 0 69 182 312 489 50 164 4 93 226 376 573 51 133 0 86 239 409 626 52 126 0 72 245 435 672 53 131 0 63 256 466 723 54 123 0 46 259 489 766 55 95 0 1 234 484 781 56 70 0 0 184 454 771 57 85 0 0 149 439 776 58 91 0 0 120 430 787 59 70 0 0 70 400 777 60 56 0 0 6 356 753 61 54 0 0 0 310 727 62 39 0 0 0 249 686 63 32 0 0 0 181 638 64 31 0 0 0 112 589
Runners "accumulate" when their arrival rate exceeds the processing rate. Otherwise, all arriving runners are assumed to be processed and any extra capacity in the processing rate goes to reduce the accumulation, if any. For example, at 43 minutes, the arrival of 110 runners is completely covered by R=120 and up. Ten runners accumulate for R=100 resulting in an accumulation of 10 since none had accumulated prior to that time. For R=80, 30 runners accumulate, adding to the 37 that had previously accumulated, bringing the total awaiting processing to 67.
After 60 minutes, the arrival rate has dropped to less than 60 rpm. Finish lines processing runners at 140 rpm or better would be "caught up" by this time, i.e., no build-up of runners awaiting processing. A finish line processing runners at 120rpm would only have 6 runners waiting. A finish line processing runners at 80 rpm would still have 753 runners waiting to be processed!
The maximum chute build-up (B) in each case can be readily determined by scanning the accumulation of finishers for each minute. A general relation can be developed if one assumes the distribution of finishers to be "normal" or to follow a "bell-shaped" curve. The "exact" solution is rather complicated. A fairly simple, more conservative guide to the maximum chute build-up (B) is given by:
EQUATION (2)
B = 0.307 N [(P/R) - 1]
where N is the total number of finishers, P is the peak arrival rate (equation 1), and R is the estimated processing rate. The maximum chute build-up (B) is given in numbers of runners. Again, this gives an overestimate to be on the safe side.
As an example of how well equation (2) predicts the maximum chute build-up (B), let's compare a theoretical 3000 person race having a normally distributed population of finishers as calculated by the "exact" method with the 1985 New York Perrier male finishers (3080) and 1985 Elizabeth River Run both male and female finishers (3061) and with equation (2) for a 3000 person race.
process "exact" Perrier River equation rate method men Run (2) 170 rpm 30 5 0 54 160 rpm 85 26 5 115 150 rpm 158 76 40 184 140 rpm 245 126 93 263 130 rpm 346 212 159 354 120 rpm 459 314 259 461 110 rpm 585 434 369 586 100 rpm 723 561 489 737 90 rpm 874 710 621 921 80 rpm 1037 889 787 1151
Note that if you plan on a particular processing rate and maximum chute build-up, equation (2) will overpredict by roughly an amount equivalent to 10 to 15 rpm in the processing rate. This is not a large safety factor and differences between experienced finish line personnel and untrained personnel will greatly exceed this difference.
Other factors affect the distribution and the maximum chute build-up. A "single-sex" race generally has a narrower distribution than a "mixed-sex" race. This means higher arrival rates near the peak and greater build-up. This is clear when comparing the Perrier men's distribution with the Elizabeth River Run mixed race. Races with qualifying times or "elite" races may be expected to yield higher peak arrival rates than would be indicated by equation (1) and correspondingly greater chute build-up.
Suppose that your last year's race was 10 km with 1,200 runners. The calculated peak density would be 72 rpm. If your processing rate is 60 rpm, the expected maximum chute build-up would be 74 runners. Allocating two runners per meter of chute, a chute length of 37 meters (120 feet) would be adequate.
Now suppose that this year's registration suggests you will have 1800 runners, a 50% increase. The calculated peak density is 108 rpm. If your processing rate remains the same at 60 rpm, the calculated maximum chute build-up is 442 runners. This would require 221 meters of chutes, i.e., a SIX FOLD increase in chute length to accommodate a 50% increase in numbers!
From this example, it is obvious that increasing chute length is NOT the answer to handling larger races. The ONLY way to handle larger races is to improve the processing rate. This can be done by selecting a faster system for processing runners in the chutes OR by parallel processing, i.e., increase the number of processing chutes or the number of finish lines.
Under the toll-booth method, the peak arrival rate for any given finish line should not exceed the processing capacity of a single sub-system for recording bib-numbers. Since processing rates generally are low, finish line back-up is not a problem for a PROPERLY designed toll-booth system. The number of finish lines for a tollbooth method is the estimated peak arrival rate DIVIDED by the processing rate for a single recording sub-system.
The second method improves the overall processing rate for a given finish line by using several processing chutes, each operating in PARALLEL. For example, using four processing chutes, each having a processing rate of 30 rpm, yields an overall processing rate of 120 rpm (provided runners are switched optimally). This second method is termed the "multi-plex" method.
In the multi-plex method, the stream of finishers must be switched from chute to chute as each chute fills up. The frequency that switches need to be made depends on how quickly runners back up.
If we assume that runners will WALK into the chutes at 80 meters per minute (3 mph) and are spaced one meter apart, then the maximum rate at which runners can enter the chutes is 80 rpm. For a marathon, you may expect a significantly slower "walk-thru" speed. Depending on weather conditions, the walk-through rate may be from 40 to 60 rpm for a marathon. You may expect slower walk- through rates for a race comprised of a high fraction of novice runners who don't know what to expect after they cross the finish line.
If the arrival rate is not greater than the walk-through rate or 80 rpm under normal conditions, all finishing runners can decelerate to a walk and enter the processing chutes. If the arrival rate is greater than 80rpm, runners will "pile-up" in the deceleration zone BEFORE entering the chutes.
Assuming that the runners arrive at the finish line at regular intervals (ignoring "clusters"), the maximum rate at which the "pileup" moves from the head of the chutes to the finish line is given by:
EQUATION (3)
U = [P -(W/S ]/[(1/S)-(P/F]
where P is the peak arrival rate (rpm), W is the "walk-thru" speed in meters per minute, S is the separation between runners in the chute in meters, and F is the finishing speed as the runners cross the finish line in meters per minute. There is no backup as long as the peak arrival rate is less than the walk-through rate which is estimated at 80 rpm. There is "instant disaster" for P greater than or equal to F/S since U becomes infinite.
For a 10 km race, the finishing speed at 45 minutes is roughly 10,000/45 or 220 meters per minute. If the peak arrival rate is 120 rpm, the "back-up" moves toward the finish line at 87 meters per minute. If the deceleration zone is 20 meters long, the build-up will reach the finish line in just under 14 seconds!
If the peak finishing rate is 150 rpm, the propagation of the build up back towards the finish line is 216 meters per minute which gives you 5.5 seconds between chute switches. This is why some races resort to increasing the length of the deceleration zone. In this case, a deceleration zone of 60 meters (rather excessive) would allow chute switching every 17 seconds. This is NOT the best solution.
According to equation (3), instant disaster would occur for peak arrival rates above 220 rpm. Unfortunately, runners tend to arrive at the finish line in "clusters" which tends to aggravate the finish line back-up problem. Middle-of-the-pack runners also tend to finish at rather different speeds, from an all-out sprint to a "survival shuffle." This suggests the REAL problem is maintaining proper finish order in the deceleration zone. More judges (physically controlling runners rather than standing around watching!) can help up to a certain point. Maintaining proper finish order for arrival rates above 100 rpm for a single finish line is very difficult.
The conclusion to be drawn from this exercise is that a single finish line for a multi-plex system SHOULD NEVER EXCEED a peak finishing rate of 120rpm! It is recommended that peak finishing rates not exceed 100 rpm.
Each "switch" would encompass 20 to 30 runners. This block of runners will be termed a "batch" in the multi-plex system and will be assumed to encompass 30 runners (to be on the conservative side).
The most efficient way of processing runners requires KEEPING THEM MOVING. Once they stop, your processing rate will drop which means an increased potential for chute build-up. This makes matters worse and pretty soon you have a non-functioning finish system.
The ideal chute length is determined by the peak arrival rate (P) and the single chute processing rate (R). If the peak arrival rate is NOT GREATER than the single chute processing rate, the chute serves simply to guide the runners past the processing station. The deceleration of the runners decreases their separation but will still permit a 60 to 80 meters per minute (2 to 3mph) walk-through rate in the chutes. Since the separation will be greater than a meter, the spacing of the runners and their walk-through speed will equal the arrival rate.
In the multi-plex system, the arrival rate much of the time will exceed the single chute processing rate. When this occurs, runners are switched from chute to chute at intervals which permit 20 to 30 runners to enter a given processing chute between each switch.
In this situation, the purpose of the chutes is to spread out the runners so that the rate at which they WALK by the recorder at the end of the chute is equal to the single chute processing rate for that method of recording finishers. If the runners cannot WALK by the recorder, some of them will be forced to STOP. Once stopped, they will be hard to get moving again which will slow the flow of runners through the chutes and reduce the processing rate.
The ideal chute length for multi-plex systems is determined by the processing rate (R), the number of runners accepted in a single batch, assumed to be 30, and the walk-through speed (W). The walk-through speed is that speed the runners walk by the recorder at the END of the processing chute. This depends on the race length and the length of the processing chutes (which will be a function of the processing rate). For short races, the walk-through speed may range from 30 to 60 meters per minute (1.1 to 2.2 mph); for a marathon, the walk-through speed may range from 20 to 40 m/min. (0.7 to 1.5 mph).
Suppose the runners are walking at 60 in/mm. and are one meter apart, they will pass by a given point at 60rpm. If they are two meters apart, they will pass by at 30 rpm. Hence, for a processing rate of 30 rpm, the runners should be spaced two meters apart. Since each batch contains some 30 runners, if they are spaced 2 meters apart, the ideal chute length for recording systems where R = 30 rpm is 60 meters.
Since runners will tend to slow more as the processing chute length increases, the ideal chute length does not increase inversely with the processing rate. The ideal chute length (L) in meters, may be estimated by:
L = 15 + (500/R)
for short races, (4) and
L = 10 + (400/R) for long (marathon) races, (5)
where R is the single chute processing rate (rpm). The walk-through rate has been assumed to be a linear function of the single chute processing rate, given by W 20 + (R/2).
A pull-tag/spindle system with a typical processing rate of 30 rpm should use 32 meter chutes for a 10 km race and 24 meter chutes for a marathon. A manual recording system with a typical processing rate of 20 rpm should use 40 meter chutes for a 10 km race and 30 meter chutes for a marathon. A place card/pull tag system with a processing rate of 80 rpm should use 21 meterchutes for short races and 15 meter chutes for a marathon.
The 1983 Bolder Boulder race employed 23 separate groups of runners seeded by their estimated time as filled out on their entry blank. Each group was identified by COLOR and by NUMBER BLOCKING. For example, a runner expecting to complete the race in 45 minutes was given a GREEN number in the 5000 block of numbers. That runner would locate the green signs indicating 5000- 5999. Groups average about 700 to 800 runners each.
Over 300 marshalls working in the staging area were responsible for making sure runners lined up with their proper group and that the groups moved to the starting line in their proper order. Groups started roughly 15 seconds apart. As each group was started (with a starting gun), the elapsed time from the first starting gun was recorded. This was later fed into the computer and all runners starting in that block had that elapsed time subtracted from their overall time.
The KEY to reliability in a wave system is to be able to conveniently spot and remove runners who DO NOT belong in a particular starting group. Color coding and number blocking PLUS plenty of marshalls are needed to make this work.
The benefits are twofold. First, each runner is given a better opportunity to run a representative time, i.e., it should not take more than a few seconds for any runner to reach the starting line. If all the runners in Bolder Boulder were started at the same time, it would take several minutes for all the runners to cross the starting line.
Second, the peak arrival rate may be reduced. This means the finish system capacity may be reduced, i.e., fewer finish lines and/or fewer processing chutes.
There are many ways that runners could be assigned to different starting times. The simplest way would be to distribute entrants randomly among several starting groups. As an example, consider a hypothetical 20,000 person 10 km race with a mean (average) time of 50 minutes and a standard deviation of 8 minutes normally distributed. Such a race may expect 68% of its finishers to arrive between 42 minutes and 58 minutes. This would produce an AVERAGE arrival rate over 16 minutes of 850 rpm (13,600 runners divided by 16 minutes). The peak of the actual distribution is 1000 rpm; that calculated by equation (1) is 1200 rpm.
Divide this race into ten identical starts, each separated by a fixed time lag, e.g., one minute or two minutes, as shown. Each start will have 2000 runners and will be normally distributed with a mean of 50 minutes and a standard deviation of 8 minutes. By "adding up" each of the ten curves for each of the ten starts, the curves shown in Figure 2 are obtained.
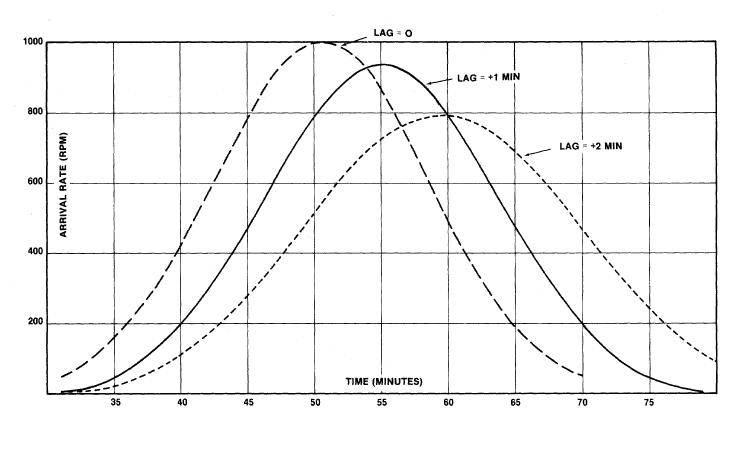FIGURE 2-2.
Theoretical distributions of finishers for a randomly assigned wave start with ten equal-sized starting groups.
A lag of zero represents a single start; a lag of one minute represents one minute gaps between starts; a two minute lag represents two minute gaps between starts.
There is a reduction in the peak arrival rate, from 1000 rpm with no lag (simultaneous start) to 925 rpm for a one minute lag between groups and to 792 rpm for a two minute lag. Note that the AREA under each curve is the SAME. The reduction is peak arrival rate is accomplished by spreading the distribution. We could get even lower peak arrival rates by spreading the distribution even more but few cities will permit ten back-to-back races, completely separated in time!
A better way is to "seed" the runners according to their projected finish time. If we start the fastest runners first and delay the start of the slower runners, we will "spread" the distribution of finishers and consequently will lower the peak arrival rate. Of course, we could start the slower runners first and the fastest runners last and "handicap" our race so that all 20,000 runners would finish together! In other words, seeded starts MUST place the fastest runners in the first start and each start should be comprising of successively slower runners.
When entering the race, each runner must "predict" a finishing time. For simplicity, assume that only predicted times in "whole" minutes are obtained, i.e., a runner who predicts a time of 50 minutes anticipates running closer to 50 minutes than 49 or 51 minutes.
In this case, EACH start has a different MEAN time associated with it and the standard deviation will be much smaller. Here, we will assume a standard deviation of 90 seconds for each one minute predicted group since it seems plausible that most runners can predict their finishing time for a 10 km race to plus or minus one minute and each group covers a range of plus or minus 30 seconds.
Again, divide the race into ten starting groups. For simplicity, in calculations as well as in actually seeding a race, each starting group will encompass several predicted times and groups will be roughly the same size. The breakdown is shown in Table IV.
TABLE IV. Assignment of Runners into Ten Equal-Sized Seeded Groups.
| Group I II III IV V VI VII VIII IX X |
Predicted Times 28 to 39 min. 40, 41, 42 min. 43, 44, 45 min. 46 and 47 min. 48 and 49 min. 50 and 51 min. 52 and 53 min. 54, 55, 56 min. 57, 58, 59 min. 60 and up |
Group Size 1893 1592 2252 1809 1956 1985 1895 2452 1815 2351 |
Now consider a positive lag of one minute between successive starts, i.e., in the desired direction of fastest first, slowest last. Each one minute predicted time group is added into the finishing distribution separately, even though several such groups may start at the same time.
FIGURE 2-3
Theoretical distributions of finishers for a seeded wave start with ten starting groups.
The results of this exercise are shown in Figure 3. The peak arrival rate is reduced to 661 rpm. This compares favorably with the random assignment for one minute lag which yields a peak arrival rate of 925 rpm. Clearly, assigning the runners by estimated finish time is worth the effort, PROVIDED it is done right. For comparison, a time lag of negative one minute (slowest first, fastest last) produces a peak arrival rate in excess of 1800 rpm!
There are better ways still! Remember that the AREA under the curve remains constant. For a given time lag, the lowest peak arrival rate would result if the arrival rate went from zero to the peak value immediately and remained there until the last finisher crosses. This means if we use LARGER groups for the first and last groups which normally have lower arrival rates anyway and SMALLER groups near the peak, we can "flatten" the distribution while keeping the overall time lag constant. Likewise, we can vary the time between starts, for example, leaving two minutes between large groups and only one minute between smaller groups.
With the constraints on assigning runners to starting groups as above, consider an example with unequal-sized starting groups. In addition, assume a two minute gap between each of the first and last four starting groups and a one minute gap between the others. The first and last groups are the largest, as shown in Table V.
TABLE V. Assignment of Runners into Unequal-Sized Seeded Groups (a "better-yet" method).
| Group I (2 min.) II (2 min.) Ill (2 min.) IV V VI VII VIII IX X (2 min.) XI (2 min.) XII (2 min) XIII |
Predicted times 28-42 min. 43-44 min. 45-46 min. 47 min. 48 min. 49 min. 50 min. 51 min. 52 min. 53 min. 54-55 min. 56-57 min. 58 min + |
Group size 3485 1432 1701 928 967 989 996 989 967 928 1701 1432 3485 |
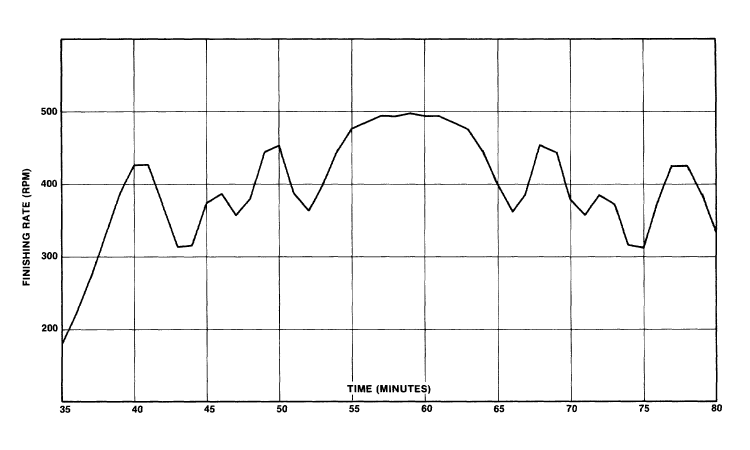FIGURE 2-4
Theoretical distributions of finishers for a "better method yet" approach.
Groups of unequal size abd different gaps in starting times are chosen to minimize the peak finishing rate. Table V gives group sizes and starting times.
As shown in Figure 4, the reduction in peak arrival rate is substantial. Whereas the one minute lag with ten equal-sized groups allowed a peak finish rate of 661 rpm, the "better-yet" method allows a peak finish rate of 498 rpm! The fluctuations in the calculated arrival rate result from separating the groups seeded by time. The distribution is "stretched" only at certain points rather than uniformly. Figure 4 also suggests that the first and last groups could be started with a smaller gap, i.e., one can "fine-tune" the wave start by trying various combinations of group size and number and starting time gaps between the groups.
As part of the design of a finish system, the wave start needs to be considered for mega-races. Simply having a wave start is NOT going to solve all the problems. A poorly designed wave start will create more problems than it solves. A properly designed wave start can substantially lessen the peak load on the finish line system. The wave start does need to be TAILORED to the particular situation.
Due to the potential for cheating inherent in the wave start by "advancing" one's starting position and thereby "running" a faster time, ALL potential age record breakers and age groups award winners should start in the FIRST group. In the above example, men over 65 and under 8, and women over 55 and under 8 would start in the first group. This would add very few runners to that group while protecting any records that may be set AND makes your awards search faster and more reliable (cheat-proof).
| Go to Next Section: | Finish Line Subsystems |
| Previous Section: | The Start |
| Back to: | Table of Contents |